How to generate a valid and fast Sudoku board from scratch?

I don’t believe I’m writing a blog post related to Sudoku since it’s already a solved problem/exercise and it’s widely known, but I wanted to share my experience and my thought thinking about creating a valid Sudoku board and what it means to have a valid Sudoku.

The Story

Before diving into my obvious task in hand, I wanted to share the before. I’m currently having my Masters education in Computer Science program in Fordham University, New York. One of my classes, Software Engineering, gave us a homework about developing a Sudoku application for a imaginary company and what are the activity diagrams for a particular task: “Generating a Sudoku board”.

Before thinking about any algorithms, I wanted to give some information about what it means to generate a Sudoku board, and a valid one.

Requirements

1. Board can be in different sizes. (Ex: 4x4, 9x9, 16x16)
2. Board should have a unique solution. If a Sudoku puzzle is solved with more than 1 approach, than it’s not a Sudoku board, it’s a puzzle? (lol)
3. Board should have some sort of understanding of what a difficulty is, or should have a basis of generating within a difficulty. (For the sake of simplicity, I won’t be covering difficulty in this post)
4. Each board cell should be unique in their corresponding row, column and their square.

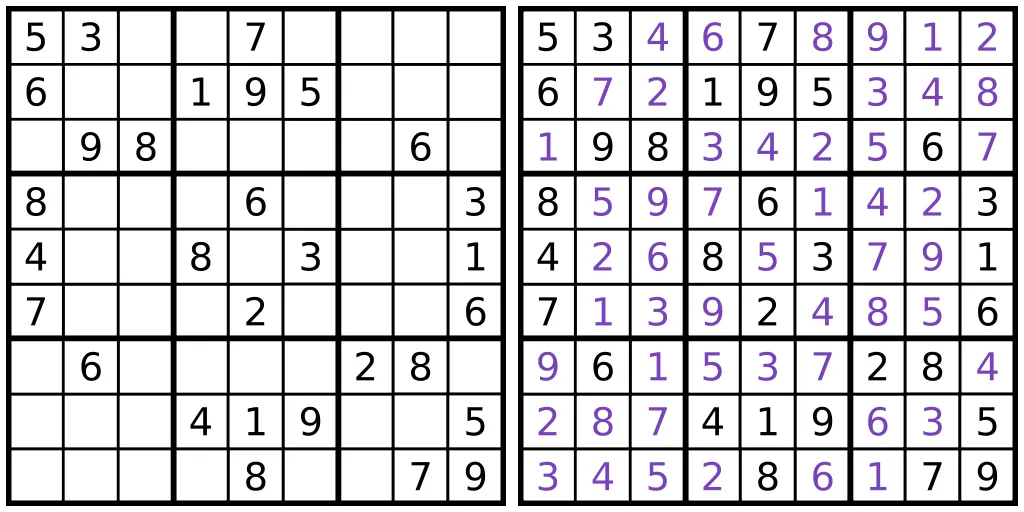
An example Sudoku puzzle with a solution

The Goal

Our goal in this blog post is to create a thought process and a basic algorithm for generating a solvable Sudoku puzzle with a unique solution and have the flexibility to introduce difficulty level later on to the algorithm.

I believe that the goal can be achieved in a reduced 2 step process.

1. Generating a full/solved Sudoku puzzle where every cell has a valid value and respects the board size.
2. Generating a uniquely solvable game board from a puzzle.

Step 1: Generating a solution

Glossary

• Square is referenced to each square inside the Sudoku board. For a 4x4 Sudoku, there is 4 squares. For 9x9, there is 9, and etc.
• Board size is referenced to the width of the Sudoku board. For 9x9, it is 9.

Assumptions

• The board size is an integer and have a value of more than 0.
• The square count is an integer and have a value of more than 0.
• Board size divided by square count should equal to the square count. (To preserve the validity of the Sudoku board)

Thought process

Let’s generate a solution by iterating through each square in the Sudoku board (where for 4x4 there is 4 square, for 9x9 there is 9) for each number and fill it one by one while checking for the validity of the cell we’re putting it.

The following algorithm is an example of Breadth first search algorithm where each node has a validity and inserted into the tree according to the rule. For more information about the algorithm please look into the Wikipedia article .

Algorithm

1. Iterate x from 1 to board_size
2. For each x, iterate from 0 to square_count, y
3. Find all available positions in the given y.
4. Filter available positions according to the forbidden positions list. (Forbidden position list is referred to an array of indexes where the current iteration tried but could not put a value due to a child having 0 valid positions for insertion)
5. Filter available positions according to my previous positions within the same x. (This preserves the validity of the Sudoku within the same x)
6. Select a random position from the filtered list. If a position exist, update the board and continue to step 2. If no positions are available for insertion, add the last value in previous positions list within the same x to the forbidden positions list, and re-iterate y-1 with the updated forbidden list.

The visual representation of inserting numbers on 2x2 board

Step 2: Generating a uniquely solvable solution

Assumptions

• An existing solution is available to use it as a base reproduced using Step 1.
• Assume a set of difficulty ranges are available according to the minimum empty cells in a game.

Algorithm

1. Select a random cell from the board. If the cell is not-empty and not-visited continue to step 2. If the cell is visited move to step 6.
2. Remove the selected cell from the game board.
3. Calculate solutions for the removed cell on the board. If the uniqueness is achieved in solutions, continue to step 4. If there are more than 1 solution to the given removed cell, undo the removal.
4. Set the current cell as visited.
5. Return to step 2.
6. Repeat step 2 until random and non-empty cell count is 0.